ÉQUATIONS ALGÉBRIQUES

ÉQUATIONS ALGÉBRIQUES

Dès la plus haute antiquité, on rencontre, à l’occasion de problèmes concrets, des exemples de résolution d’équations du premier et du second degré, et, jusqu’au début du XIX^e siècle, l’étude des équations constitue l’unique préoccupation des algébristes.

Le développement de la théorie est étroitement lié aux extensions successives de la notion de nombre : introduction des nombres négatifs, des nombres irrationnels, tandis que les formules de résolution de l’équation du troisième degré allaient conduire les algébristes italiens du XVI^e siècle à raisonner sur les nombres imaginaires (cf. nombres COMPLEXES).

Par analogie avec le cas des équations de degré inférieur ou égal à 4, les algébristes pensèrent que toute solution d’une équation pouvait s’exprimer par des radicaux portant sur les coefficients de l’équation. Par un hasard de l’histoire des sciences, les tentatives pour établir cette conjecture, pourtant mathématiquement saugrenue, allaient conduire à dégager les premières structures abstraites et être à l’origine de l’algèbre moderne ^{[cf. ALGÈBRE]}.

1. Équations affines

On étudiera en premier lieu le développement historique des systèmes d’équations affines.

Premier exemple

Problème 69 du Papyrus Rhind (Égypte), vers 1700 avant notre ère: «Trois boisseaux et demi de farine sont transformés en 80 pains. Dis-moi combien chaque pain contient de farine et quelle est leur force.»

Rappelons que le boisseau (heqat ) mesure environ 4,5 litres. Il est divisé en 1/2, 1/4, 1/8, 1/16, 1/32, 1/64 de boisseau et contient 320 «ros» (ou parties). La «force» d’un pain est la quantité de pains que peut fournir un boisseau de farine. Si x est cette force et si y est la quantité de farine contenue dans un pain, x et y sont – avec les mêmes unités – inverses l’un de l’autre. Le texte donne pour la force:

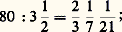et, pour la quantité de farine contenue dans un pain, 3 boisseaux et demi divisés par 80, ou 1 120 ros divisés par 80, donnent 1/32 de boisseau et 4 ros.

C’est un problème très élémentaire du type ax = b ou a = by. Toute la difficulté provient, au point de vue concret, du choix des unités de mesure et de leurs subdivisions, et, au point de vue abstrait, du calcul égyptien des fractions. Dans ce calcul, la notion de fraction générale n’est pas encore dégagée, ou, en langage actuel, l’ensemble Q⁺ n’est pas mis en évidence. À part la fraction 2/3, l’Égyptien ne calcule que par quantièmes ou fractions de numérateur 1. Ces errements se prolongeront très longtemps dans les littératures mathématiques grecque (collection héronienne), byzantine et occidentale.

Deuxième exemple

On peut trouver en Égypte des problèmes plus savants que le précédent, qui se ramènent au même type d’équation. Prenons cependant, dans la mathématique babylonienne, un deuxième exemple à peu près contemporain du précédent (E. Bruins et M. Rutten, Textes mathématiques de Suse ): «Un quart de la largeur, ajoute à la longueur: 7 mains... à 10... 10 c’est la somme. Largeur?» En désignant la longueur par x , la largeur par y , on obtient le système x + y /4 = 7; x + y = 10. Voici la solution donnée dans la tablette: «Porte 7 à 4 du «quart»: 28 tu trouves; tu soustrais 10 de 28: 18 tu trouves. Dénoue l’inverse de 3: 20 tu trouves; porte 20 à 18: 6 tu trouves: 6 la longueur; tu soustrais 6 de 10: 4, la largeur...»

Ce système de deux équations à deux inconnues est résolu suivant un procédé encore utilisé dans notre enseignement élémentaire. La numération utilisée est à base 60. La division est remplacée par la multiplication par l’inverse du diviseur.

Troisième exemple

La littérature chinoise offre, dans le même ordre d’idées, des exemples ultérieurs, parmi lesquels le suivant, extrait de Neuf Chapitres sur l’art du calcul , ouvrage qui se situe dans les deux derniers siècles avant notre ère. «Les poids de deux gerbes d’une récolte A, de trois gerbes d’une récolte B, de quatre gerbes d’une récolte C sont supérieurs à une unité de poids. Deux gerbes A valent, en sus de l’unité, une gerbe B. Trois gerbes B valent, en sus de l’unité, une gerbe C, et quatre gerbes C, une gerbe A. Quel est le poids d’une gerbe de chaque récolte?»

Le système d’équations à résoudre peut s’écrire:

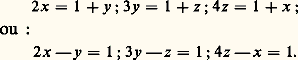Le calculateur chinois dispose sur un échiquier trois colonnes qui vont représenter les trois équations. Sur la première à droite, il place en première ligne deux bâtonnets de couleur (2x ), en deuxième ligne un bâtonnet noir (face=F0019 漣y ), en quatrième ligne un bâtonnet de couleur: 1 unité.

Il procède de façon analogue pour les autres colonnes. Doublant la colonne de gauche et lui ajoutant celle de droite, il arrive à la nouvelle disposition:

Triplant la nouvelle colonne de gauche et lui ajoutant la colonne centrale, il obtient la disposition:

On voit ainsi que 23 z = 10, et z = 10/23, puis 3 y 漣 10/23 = 1, d’où y = 11/23, et 2 x 漣 11/23 = 1, d’où x = 17/23.

Cette solution, très remarquable, nécessite que tous les coefficients dans les équations soient des nombres entiers. Elle implique la connaissance des nombres négatifs. L’ouvrage d’où elle est extraite donne d’ailleurs les règles des signes pour les deux opérations fondamentales. Enfin le calculateur tilise les fractions dans leur généralité. En résumé, les mathématiciens chinois travaillaient, pour les systèmes d’équations affines, sur le corps Q des nombres rationnels.

Simple et double fausses positions

On trouve, dans Neuf Chapitres sur l’art du calcul , nettement expliquées, les deux règles de la fausse position simple, et de la double fausse position: lorsqu’un problème conduit pour nous à une équation ax = b , le calculateur, qui ne dispose pas du calcul littéral, est souvent très gêné pour trouver le coefficient a. S’il connaît le terme b , il effectue, sur une «fausse position» x ⁰ mise à la place de l’inconnue x , tous les calculs proposés dans le problème. Il obtient ainsi une valeur b ⁰: ax ⁰ = b ⁰. Il ne lui reste plus qu’à résoudre la «proportion»:

Dans d’autres cas plus compliqués, il lui est difficile de calculer les deux coefficients a et b. Une première position x ⁰ donne ax ⁰ 漣 b = r ⁰; r ⁰ est l’erreur. Une seconde position x ¹ donne ax ¹ 漣 b = r ¹; r ¹ est une seconde erreur. Les facteurs a et b ne sont pas connus, mais les quatre nombres x ⁰, x ¹, r ⁰, r ¹ le sont.

Le calcul de x se fait alors par annulation du déterminant:

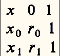c’est-à-dire que:

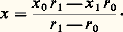Bien attestées dans l’ancienne mathématique chinoise, les règles de fausse position sont connues des Arabes et de l’Occident sous le nom d’al-khatayn (la chinoise). Elles existent toujours: c’est l’interpolation linéaire.

Indiquons enfin que les systèmes d’équations affines se rencontrent dans la littérature grecque, principalement chez Diophante d’Alexandrie (III^e siècle env.). Ce n’est d’ailleurs qu’un aspect mineur de l’œuvre du grand algébriste. Diophante ne procède pas par fausses positions. Il utilise une inconnue, pour laquelle il dispose d’une notation et d’une dénomination.

Les algébristes de la Renaissance

Au XV^e siècle, l’Italien Pacioli (1494) et le Français Nicolas Chuquet (1484), entre autres, s’intéressent particulièrement aux systèmes d’équations affines. Le premier de ces deux algébristes utilise parfois une inconnue privilégiée, la cosa , et parfois même une seconde, la quantita. Cela lui permet la résolution de systèmes à plusieurs inconnues.

Chuquet note l’inconnue l¹ et résout à notre façon les problèmes affines à une seule inconnue. Pour les problèmes à plusieurs inconnues, en plus des méthodes traditionnelles, il lui arrive d’introduire soit une, soit deux inconnues privilégiées notées alors respectivement l¹ et l². D’autre part, Chuquet utilise habilement les nombres négatifs. Il rejoint en cela les algébristes chinois et indiens, dépassant de beaucoup les quelques essais timides des savants occidentaux en la matière. Il faut cependant citer, parmi ses précurseurs en ce domaine, Léonard de Pise (XIII^e siècle).

En cette fin du XV^e siècle toutefois, la distinction entre systèmes déterminés et indéterminés n’est pas claire. En particulier, on ne voit pas précisément si le problème doit, pour être possible et déterminé, contenir plus, autant ou moins d’équations que d’inconnues.

Le XVI^e siècle apporte des progrès appréciables. L’Allemand Michael Stifel (1487-1567) note en 1544 l’inconnue d’un signe particulier analogue à r , mais, lorsqu’il se présente d’autres inconnues, il les désigne par les premières lettres de l’alphabet A, B, etc. Les données sont bien entendu numériques (appartenant à Q⁺). Il est imité, en France, par Jacques Peletier (1517-1582) dans son Algèbre , de 1554. Jean Borrel, ou Buteo (1492-1572), est plus net encore en 1559. Soit à résoudre le problème: «Étant donné une somme quelconque, trouver trois nombres dont le premier avec la moitié, le second avec le tiers, le troisième avec le quart des autres font chacun cette somme.» Il désigne les nombres par A, B, C, et, 17 étant la somme, il écrit:

Procédant alors exactement à la chinoise, il résout très clairement le système.

Lorsque dans un système affine les données sont rationnelles et les inconnues, par leur nature, entières, le système est dit diophantien. Il est généralement impossible si le nombre des équations est égal ou supérieur à celui des inconnues. Dans le cas où il y a moins d’équations que d’inconnues, il est indéterminé. La première étude scientifique des systèmes affines diophantiens est due à Bachet de Méziriac, en 1624. Il montre en particulier que, si les entiers a et b sont premiers entre eux, il existe des entiers x et y tels que ax + by = 1.

À part cela, le XVII^e siècle apporte peu dans la théorie des équations affines, sinon le développement par Descartes du calcul littéral de Viète. Cependant Leibniz entrevoit le calcul matriciel. Au siècle suivant, le Suisse Gabriel Cramer (1704-1752) fait la première étude exhaustive des systèmes d’équations affines (1750). Avec le XIX^e siècle apparaît le calcul des déterminants, puis le calcul matriciel. Ces problèmes sont à l’origine de l’étude des espaces vectoriels et de toute l’algèbre linéaire.

2. Le second degré

L’histoire des équations quadratiques: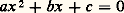

remonte, comme celles des équations affines, à des époques très reculées. La mathématique égyptienne n’a pratiquement rien découvert en ce domaine. Au contraire, l’on doit beaucoup, l’essentiel même, aux Babyloniens.

Premier exemple

Sur une tablette de l’ancien âge babylonien (YBC 4663), on demande de trouver un rectangle, connaissant son demi-périmètre, 6⁰ 30 , et son aire, 7⁰ 30 .

Il s’agit donc de résoudre le système:

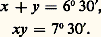Voici la méthode proposée par le scribe (numération à base 60): prendre la moitié de la longueur et de la largeur:

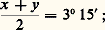élever au carré:

en retrancher l’aire:

prendre la racine carrée: 1⁰ 45 ; ajouter la demi-somme: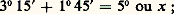

retrancher:

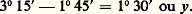Second exemple

Problème 7 de la tablette BM 13901, remontant à l’ancien âge babylonien, 1800 environ avant notre ère: «J’ai additionné sept fois le côté de mon carré et onze fois la surface: 6⁰ 15 .» Soit 11 x ² + 7 x = 6⁰ 15 .

Solution: «Tu inscriras 7 et 11. Tu porteras 11 à 6⁰ 15 : 1 8⁰45 . Tu fractionneras en deux 7: 3⁰ 30 . Tu croiseras 3⁰ 30 et 3⁰ 30 : 12⁰15 . À 1 8⁰45 tu ajouteras 1 21⁰, qui est le carré de 9. Tu soustrairas 3⁰ 30 , que tu as croisé, de 9: tu inscriras 5⁰ 30 . L’inverse de 11 ne peut être dénoué. Que dois-je poser à 11 qui me donne 5⁰ 30 : 30 , son quotient. Le côté du carré est 30 .»

À savoir: l’équation à résoudre est ax ² + bx = c. On calcule b ²/4, puis b ²/4 + ac , dont la racine est 連(b ²/4 + ac ). On forme 連(b ²/4 + ac ) – b/ 2. Le coefficient a n’ayant pas d’inverse dans l’anneau des nombres exprimables en base 60, on divise par a , par tâtonnements, 連(b ²/4 + ac ) – b/ 2. Le quotient est le côté cherché. La numération est sexagésimale: 1 + 60⁰, et 1 = (1/60). 1⁰.

D’autres exemples, fort nombreux, montrent que le calculateur babylonien sait résoudre toutes les équations quadratiques. Il y a pourtant un obstacle: ce calculateur ne s’exprime pas dans R, corps des réels, mais dans un sous-anneau, celui des nombres exprimables d’une façon finie, en base 60. Pour que ax ² + bx + c = 0 ait des racines, il ne suffit donc pas que b ² 漣 4 ac 閭 0, mais il faut encore que cette quantité soit le carré d’un élément de l’anneau et que, de plus, la division finale par a soit possible dans l’anneau.

Les Grecs font, de la résolution des équations du second degré, la base même de toute leur géométrie. Mais, pour pouvoir travailler dans R, ils remplacent les calculs babyloniens par des constructions à la règle et au compas. Pour qu’une équation quadratique ait alors des racines, il suffira que b ² 漣 4 ac 閭 0.

Le fait de construire les solutions des problèmes à partir des segments donnés, à la règle et au compas, conduit les géomètres grecs à l’étude des binômes, segments dont les mesures sont de la forme 連a + 連b , a et b rationnels. Cette étude savante n’aboutit guère à des conclusions définitives. Elle occupe cependant une grande partie des Éléments d’Euclide et joue un rôle important dans le développement de la théorie des équations. Cependant les algébristes grecs calculent dans Q, plus précisément dans Q⁺. Pour eux, une condition supplémentaire s’impose: b ² – 4 ac doit être le carré d’un rationnel. Toute l’algèbre diophantienne trouve là son origine. Elle est tenue à manipuler des équations indéterminées où certaines expressions doivent être des carrés parfaits dans Q. L’extraordinaire habileté de Diophante en ce domaine sera un très puissant stimulant pour les mathématiques des XVI^e et XVII^e siècles.

Les Arabes et leurs disciples occidentaux jusqu’au XVI^e siècle n’apportent rien d’essentiel. La nécessité de calculer dans Q⁺ ou dans R⁺ les conduit au contraire à distinguer dans les équations quadratiques de multiples cas, assez inutilement. Tout au plus savent-ils que l’équation peut, parfois, admettre deux racines (positives).

3. Équations de degré 3 et 4

Les équations cubiques

Quelques exemples d’équations cubiques apparaissent chez les Babyloniens, mais sans rien de systématique. Archimède discute (De la sphère et du cylindre , livre second) les problèmes qui, pour nous, conduisent à l’équation cubique générale. Mais sa démarche est purement géométrique et ne peut pas se traduire en algèbre. Le XV^e siècle connaît quelques tentatives malheureuses de résolution algébrique. Il était réservé à l’école italienne du XVI^e siècle d’apporter la solution définitive. Les trois pionniers sont successivement Scipione del Ferro, Tartaglia et Cardan.

L’équation générale se ramène à des formes telles que x ³ + px + q = 0. (Les algébristes n’écrivant que des coefficients numériques et positifs, trois cas sont à distinguer: x ³ = x + 1, x ³ + x = 1 et x ³ + 1 = x. )

La solution trouvée se résume pour nous dans la formule:

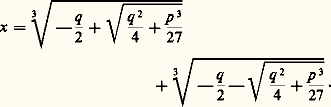Elle est obtenue en posant x = u + v , puis u ³ + v ³ = 漣 q , uv = p /3, d’où u ³ + v ³ = 漣 q , u ³v ³ = 漣 p ³/27; u ³ et v ³ sont donc racines d’une équation quadratique.

Cardan comprend aussitôt les difficultés soulevées par cette solution. Lorsque q ²/4 + p ³/27 est négatif, les nombres u et v ne peuvent pas être calculés dans R, donc n’existent pas. Or, Archimède a montré que, dans ce cas, l’équation cubique proposée a des racines, et Cardan, en acceptant les racines négatives, sait en outre qu’elle en a trois. Pour lever la difficulté, il introduit timidement, et Bombelli le fera plus nettement en 1572, de nouveaux nombres dits «impossibles» ou «imaginaires». Ainsi apparaît, pour la première fois, le corps C des nombres complexes (cf. nombres COMPLEXES).

Le quatrième degré

Un disciple de Cardan, Ferrari, résout l’équation du quatrième degré. Soit par exemple à résoudre x ⁴ + 6 x ² + 36 = 60 x. Ajoutons 6 x ² aux deux membres pour que le premier soit un carré parfait. Il vient (x ² + 6)² = 6 x ² + 60 x. Formons:

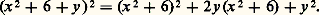L’équation s’écrit:

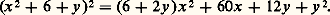Si le trinôme en x du second membre est un carré parfait (ax + b )², l’équation se ramènera au second degré: x ² + 6 + y = ax + b . Pour cela, il faut que:

Le paramètre y est donc obtenu par la résolution d’une équation cubique. C’est Bombelli qui, en 1572, étend le procédé de Luigi Ferrari à l’équation la plus générale de degré 4.

L’obligation de n’avoir dans les équations que des coefficients positifs rend la démarche de ces auteurs fort pénible.

4. La théorie «générale» des équations

Grâce à l’école italienne, la théorie générale des équations algébriques se précise et ses problèmes principaux se dégagent. Sans suivre chronologiquement son développement historique, on peut s’efforcer d’en mettre en évidence les points importants. L’équation étant mise sous la forme P(x ) = 0, l’importance du degré du polynôme P, ou degré de l’équation, apparaît d’abord; en effet, l’équation n’a pas en général une seule racine, comme le voulaient les anciens algébristes, mais peut en avoir jusqu’à n , si n est son degré.

Si a est une racine, alors P(x ) est divisible par x 漣 a et l’on peut écrire:

Q étant un polynôme de degré n 漣 1.

Si l’équation admet exactement n racines, il est possible d’exprimer les coefficients du polynôme P(x ) par des fonctions symétriques rationnelles entières des racines.

Exemple du second degré:

de racines a et b ; alors:

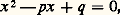
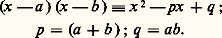Exemple du troisième degré: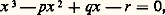

de racines a , b , c ;

Exemple du cinquième degré:

de racines a , b , c , d , e ;

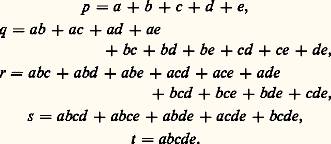Ces relations apparaissent déjà chez Viète, dans le seul cas où toutes les racines sont positives, mais c’est Harriot, en 1630, dans ses œuvres posthumes, et surtout Albert Girard, en 1629, qui leur donnent toute leur extension. Girard, d’autre part – et il sera suivi par Newton – exprime les sommes des puissances des racines en fonction des coefficients:

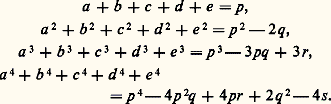L’étude des fonctions symétriques des racines se développe considérablement au XVIII^e siècle avec Waring, au XIX^e avec Cauchy, etc.

Ces belles relations ne sont évidemment établies, chez Viète, que lorsque toutes les racines sont positives, et, pour tout algébriste, que si elles existent. Tout dépend du sens donné au mot «existence». Pour Jean de Beaugrand par exemple, vers 1638, exister est synonyme d’«appartenir à l’ensemble R des réels». Pour Girard, on peut admettre des «solutions impossibles» pour la «certitude de la règle générale et pour son utilité». Pour Descartes, en 1637, «les racines ne sont pas toujours réelles, mais quelquefois seulement imaginaires, c’est-à-dire qu’on peut bien toujours en imaginer autant que j’ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celle qu’on imagine». Il semble bien que ce soit Peter Roth de Nuremberg qui ait, le premier, en 1608, énoncé cet aphorisme hardi: «Une équation a autant de racines qu’il y a d’unités dans son degré.» Cette conclusion est une conséquence des principes énoncés par Bombelli, sans leur être identique. Cet algébriste italien introduit 連漣 1, qu’il adjoint aux nombres réels, créant ainsi le corps C des nombres complexes. Il peut alors retrouver les racines réelles de l’équation cubique dans le cas dit «irréductible». Roth, suivi par Girard et Descartes, puis par la grande majorité des mathématiciens, décide, très arbitrairement, l’existence d’êtres fictifs, n’appartenant pas à l’ensemble R des nombres réels (et dont on ignore s’ils appartiennent ou non à C), et étend à ces êtres les algorithmes classiques de calcul. Jusqu’en 1746, on maniera ainsi des êtres imaginaires, sans trop savoir quelle pourrait bien être leur structure. Cependant la conviction se répandait de plus en plus qu’ils étaient de la forme a + b 連漣 1. C’est ce que d’Alembert établit cette année-là, en s’appuyant sur le calcul infinitésimal et la géométrie analytique et en admettant le principe d’existence des n racines d’une équation de degré n. Daviet de Foncenex, Lagrange, Laplace améliorèrent cette démonstration, mais en se fondant toujours sur le même principe. Gauss, en 1799, qualifia de cercle vicieux cette démarche et il fournit enfin plusieurs preuves rigoureuses du «théorème fondamental de l’algèbre», ou « théorème de d’Alembert ».

On sait aujourd’hui que l’attitude des géomètres du XVIII^e siècle peut se justifier en ce domaine, et cela, grâce à la théorie des congruences de Gauss et à l’introduction par Galois du corps de rupture. Précisons en quelques mots. Soit un corps K, commutatif, et un polynôme P(x ), indécomposable sur K en un produit de deux polynômes (premiers sur K). Alors l’anneau des polynômes construits sur K se subdivise en classes d’équivalences: deux polynômes R(x ) et S(x ) sont équivalents si leur différence est divisible par P(x ). On démontre que ces classes d’équivalence forment un corps commutatif. Désignant par a la variable désignée par x jusqu’ici, tous les éléments du corps sont des polynômes en a à coefficients dans K.

Dans ce nouveau corps, P(a ) 令 0; autrement dit, P(x ) admet la racine a et est divisible par x 漣 a.

Exemple. En prenant, pour P(x ), x ² + 1, et, pour K, le corps R des réels, et en notant i ce que nous notions a , on trouve le corps des complexes où x ² + 1 = (x + i ) (x 漣 i ). Cette construction du corps des nombres complexes a été proposée par Cauchy.

De ce point de vue, la démarche des précurseurs de Gauss était correcte. Le seul point à établir était de montrer que, pour K = R, P(x ) premier quelconque, le corps de rupture est un sous-corps de C.

5. Résolution numérique

Pour une équation P(x ) = 0, les questions suivantes se sont posées naturellement: Combien a-t-elle de racines réelles? Combien d’imaginaires? Combien de positives, de négatives? Quelles sont les valeurs approchées, au 1/10, au 1/100, au 1/1000 près, etc. de ces diverses racines?

Descartes, dans sa Géométrie de 1637, déclare, sans preuves, que l’équation P(x ) = 0 peut avoir autant de racines réelles positives qu’il y a de changements de signe dans les monômes du premier membre ordonné, et autant de négatives qu’il y a de permanences.

Ainsi x ⁴ + x ³ 漣 x ² + x + 1 = 0 peut avoir deux racines positives et deux racines négatives. En fait, cette équation n’a aucune racine positive et deux racines négatives, les deux autres étant imaginaires conjuguées. On énonce aujourd’hui le théorème de Descartes comme il suit: Dans une équation quelconque, à coefficients réels, le nombre des racines positives ne surpasse pas le nombre des variations de signe du premier membre; et, quand il est moindre, la différence est toujours un nombre pair.

En 1690, Rolle (1652-1719) énonce dans son Algèbre une proposition que l’on peut exprimer ainsi: Soit P(x ) = 0, formons l’équation P (x ) = 0, P étant le polynôme dérivé du polynôme P. Entre deux racines de la première équation, il existe au moins une racine de la seconde.

Le théorème de Budan (1811) se rattache au même ordre d’idées: «Étant donné une équation P(x ) = 0 de degré m , si dans les (m + 1) fonctions P(x ), P (x ), P (x ), ..., P^{(m )}(x ) où chacune est la dérivée de la précédente, on substitue à x deux nombres 見 et 廓 ( 見 麗 廓), et, si après chaque substitution on compte les variations de signe que présente la suite des résultats, le nombre des racines de P(x ) = 0 comprises entre 見 et 廓 ne surpasse jamais celui des variations perdues de 見 à 廓, et, quand il est moindre, la différence est toujours un nombre pair.»

Le théorème de Sturm (1829) est le résultat le plus précis qui ait été obtenu dans ce domaine. Soit P(x ) = 0 l’équation proposée. On divise P par le polynôme dérivé P . Soit P² le reste euclidien changé de signe. Divisons P par P², et soit P³ le reste changé de signe, etc. Si m est le degré de P, supposé sans racines multiples , considérons la suite P, P , P², P³, ..., P^m . Soit alors, comme dans le théorème de Budan, 見 et 廓 ( 見 麗 廓) deux nombres donnés. Formons P( 見), P ( 見), ..., P^m ( 見), et de même P( 廓), P ( 廓), ..., P^m ( 廓).

Le nombre des racines de l’équation comprises entre 見 et 廓 est précisément égal à l’excès du nombre des variations de signe que présente la première suite sur celui que présente la seconde.

Les théorèmes précédents et quelques autres analogues permettent la séparation des racines de l’équation. C’est-à-dire que, pour chaque racine réelle, on arrive à trouver deux nombres 見 et 廓 entre lesquels il n’existe que cette racine de l’équation. À partir de là, on peut appliquer les méthodes générales de résolution d’une équation f (x ) = 0 (cf. analyse NUMÉRIQUE) pour obtenir des valeurs approchées des racines.

6. La résolution algébrique des équations

Par cette expression, on entend traditionnellement la résolution des équations au moyen de radicaux carrés, cubiques, etc.

On a vu que sont résolubles par ce procédé les équations de degrés 2, 3 et 4. Après les succès de l’école italienne au XVI^e siècle, les mathématiciens se sont attachés à trouver des formules de résolution analogues pour les degrés suivants, singulièrement pour le cinquième. Parmi les recherches les plus remarquables en ce domaine, on peut citer celles de Tschirnhaus (1651-1708). Il s’efforce, en 1689, par un changement de variable, de ramener toute équation algébrique à une équation binôme. Plus précisément, soit P(x ) = 0 une équation de degré n . Posons y = Q(x ), Q étant un polynôme de degré n 漣 1 à coefficients indéterminés. On élimine x entre les deux équations P(x ) = 0 et Q(x ) 漣 y = 0, et l’on détermine les coefficients du second polynôme de façon à faire disparaître, dans l’équation résultante en y , certains ou tous les termes intermédiaires. Si la méthode de Tschirnhaus réussissait toujours, toute équation serait algébriquement résoluble. Au XVIII^e siècle, Euler et Bezout ont étudié le même problème par des procédés analogues.

Un mémoire de Vandermonde, lu en novembre 1770, devait inaugurer une ère nouvelle. Kronecker n’a pas craint d’affirmer que l’essor moderne de l’algèbre commençait avec ce mémoire. Vandermonde y apparaît comme le précurseur et le premier ouvrier de la théorie des substitutions, distinguant, avant Gauss et Abel, les fonctions cycliques invariantes par une permutation circulaire déterminée et décomposant les fonctions symétriques en fonctions cycliques. Naturellement, il n’aboutit pas pour les degrés 5 et 6, mais il montre combien il serait prématuré de conclure à l’impossibilité de la résolution des équations générales de degré supérieur à 4. Puis il note que, si sa méthode échoue pour ces équations générales, elle réussit pour des équations particulières dont les racines sont liées par certaines relations et il prend pour exemple x ¹¹ 漣 1 = 0, dont il exprime les solutions au moyen de racines carrées et de racines cinquièmes.

Avec Vandermonde apparaît ainsi la notion de substitution dans un ensemble fini, celui des racines d’une équation algébrique, notion que devaient approfondir les algébristes ultérieurs, et dont l’étude aboutira, avec Galois, au concept nouveau de groupe fini.

Les idées développées par Vandermonde se trouvent encore, indépendamment d’ailleurs, dans l’important mémoire de Joseph Lagrange, lu en 1771: Réflexions sur la résolution algébrique des équations.

Gauss, dans ses Disquisitiones arithmeticae (1801), explicite les remarques de Vandermonde sur les équations binômes x ⁿ 漣 1 = 0, les appuie solidement sur les propriétés arithmétiques de l’exposant et montre notamment, à partir de l’équation x ¹⁷ 漣 1 = 0, la possibilité d’inscrire dans le cercle, à la règle et au compas, un polygone régulier de 17 côtés.

Les travaux de Vandermonde, Lagrange et Gauss attirèrent en particulier l’attention des géomètres sur les fonctions entières de plusieurs variables et sur les changements qu’elles éprouvent dans une permutation de ces variables. Lagrange démontra que le nombre des valeurs d’une fonction de n lettres est toujours un diviseur de n !, produit des n premiers entiers. Ruffini (1765-1822) établit en 1799 que si une fonction de cinq variables a moins de cinq valeurs distinctes, elle ne peut en avoir plus de deux. Si ce théorème n’établit pas l’impossibilité de la résolution algébrique de l’équation générale du cinquième degré, il prouve du moins l’impossibilité de former une équation auxiliaire ou résolvante de degré inférieur à 5. Cauchy généralise: Si une fonction de n lettres a moins de p valeurs distinctes (p plus grand nombre premier contenu dans n ), elle ne peut en avoir plus de deux (1815).

Ces diverses propositions nécessitaient déjà l’étude de la structure de l’ensemble des substitutions de n lettres, en particulier celle des substitutions circulaires.

Abel (1802-1829), dans le même ordre d’idées, avait établi qu’une fonction de 5 lettres ayant cinq valeurs distinctes est symétrique par rapport à 4 lettres. Appliqué à la résolution algébrique des équations, ce théorème montrait que, si l’on cherche à faire dépendre la résolution de l’équation générale du cinquième degré de celle d’une résolvante de ce même degré, on revient à la transformation de Tschirnhaus. Ruffini énonça en 1813 l’impossibilité de la résolution algébrique de cette équation générale du cinquième degré. En 1824 et 1826, Abel apporta sur ce point des arguments plus probants. De plus, généralisant l’analyse de Vandermonde et de Gauss pour les équations binômes, il établit que, si deux racines d’une équation irréductible sur le corps des coefficients sont telles que l’une puisse s’exprimer rationnellement par l’autre, l’équation est résoluble par radicaux si son degré est un nombre premier, et que, s’il n’est pas premier, sa résolution dépend d’équations de degrés moindres que le sien.

Abel, dans son étude de l’équation du cinquième degré, se servait du fait que les quantités successives dont il faudrait, dans cette résolution, extraire les racines n -ièmes doivent s’exprimer rationnellement en fonction des racines cherchées. Ce point présente des difficultés. Galois (1811-1832) procède par une démarche différente (1830). En appelant groupe d’une équation, sur un corps donné, le groupe des permutations de ses racines qui laissent inchangées les expressions polynomiales des racines dont la valeur appartient à ce corps, il montre que, dans une résolution par radicaux, et dans les réductions successives que subit, au cours des calculs, le groupe de l’équation, chaque nouveau groupe est un sous-groupe invariant du précédent. Or, le groupe des substitutions de cinq lettres n’a pas de sous-groupe invariant. Donc la résolution algébrique de l’équation générale du cinquième degré est impossible. De plus, sa méthode lui permit (1831) de montrer que, pour qu’une équation irréductible de degré premier soit soluble par radicaux, il faut et il suffit que, deux quelconques des racines étant données, les autres s’en déduisent rationnellement (cf. CORPS [mathématiques]).

À un point de vue plus élémentaire, mais historiquement très important, signalons le mémoire du mathématicien français Pierre Laurent Wantzel (1814-1848): «Recherches sur les moyens de reconnaître si un problème de géométrie peut se résoudre par la règle et le compas » (1837). Wantzel y montre pour la première fois, d’une façon irréfutable, que, si un problème de géométrie conduit à une équation de troisième degré, indécomposable sur le corps de ses coefficients, ce problème n’est pas résoluble à la règle et au compas. Ainsi se trouve justifiée la distinction grecque entre les «problèmes solides», comme ceux de la duplication du cube et de la trisection de l’angle, et les «problèmes plans», traitables à la règle et au compas.

Encyclopédie Universelle. 2012.